I don't think there is a more beautiful line in the world than the curve described above. Zeising went so far as to claim for the Golden ratio that;
"... [It is] the universal law in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form."Well actually the nautilus shell is not a true Phi-spiral, but it's pretty close so we'll go with Zeising's effusiveness for now. This is Part IV in the series How to Draw the Acanthus, and deals with the topic of how to draw a volute, or acanthus scroll.
I don't mean to mislead with the opening image, but in this instance we are going to look specifically at the Ionic volute (not the curve described by the logarithmic spiral above). I have linked out in this article to other mathematical scrolls if you're interested in further reading regarding Fibonacci numbers, Golden Spiral, or logarithmic spirals.
But first, a little background. The following quote is from Elements of Geometrical Drawing, by John Henry Spooner (1901), describing the Ionic volute.
 |
| Erechtheum capital from Stuart and Revett’s The Antiquities of Athens (1790) |
James Stuart and Nicholas Revett’s The Antiquities of Athens (1790) was the book that popularized the Ionic order of the Erechtheum through it's beautiful illustrations. Historian Calder Loth points out that "The Erechtheum’s volutes are the most complex of all Greek Ionic capitals, having a series of tightly spaced creases or canals resembling fine drapery. The central swag in the canals, a characteristic feature of Greek Ionic capitals, emphasizes the drapery-like character."
 |
| Corinthian Acanthus Scroll |
The volute made it's way into the Corinthian order too. A Textbook on Ornamental Design (1901) introduces the Choragic monument of Lysicrates in Athens as "the principal structure of Greek origin designed in the Corinthian order", and describes the section of Acanthus scroll pictured above as showing...
So we're beginning to see the importance of the scroll design, whether as described by the natural roll of a fern or shell, as evidenced in Greek, Roman or Islamic architecture, or as a mathematical design principle adopted by the likes of Le Corbusier. It seems we should probably learn how to draw one of these things then, right?"... not only the elaboration of ornament characteristic of this order, but also a principle of ornamental design that is of the utmost importance in its relation to the lack of invention of new forms and the restraining influences of certain art periods. It will be observed here that the various parts of the acanthus scroll grow out of one another in a continuous line. This is a principle of design that originated with the Greeks, and was continued by the Romans."
There is ample historic precedent for drawing the volute, but oddly the information seems to vary. A number of different methods are described in The New Metal Worker Pattern Book, by George Watson (1901). Spooner maintains that the ratio for describing it's curve is 7 : 6 : 5, and claims that the Greeks would agree. Another source follows a ratio of 6.5 : 5.5 : 4.5. [Though I am strictly a layman, these ratios seem like approximations to me; 7 : 6 is surely not the same as 6 : 5, nor is 6.5 : 5.5 as 5.5 : 4.5 (but please feel free to enlighten me). A more accurate Ionic ratio would be 7 : 6 : 5.143, which is what I will use here].
The point is that although the ratios may change, our method for constructing the volute remains the same. We could substitute 7 : 5.5 : 4.321 (which would describe a different curve) just as easily, but for now we will concentrate on drawing the distinctive ram's horn shape of the scrolls of an Ionic capital as described by Spooner's ratio.
Here are the steps you need to follow:
 |
| Fig. 1 |
 |
| Fig. 2 |
Step 2: So, according to the traditional ratio of 7 : 6 : 5.143, we divide the length of AB by 1.1666666666 to give us the length of BC. [In the case of the ratio 6.5 : 5.5 : 4.5, we would divide by 1.1818181818].
Continuing in this manner, we determine the length of CD [Fig. 2], by dividing BC by 1.1666666666. This gives a length for CD of 2.57cm .
 |
| Fig. 3 |
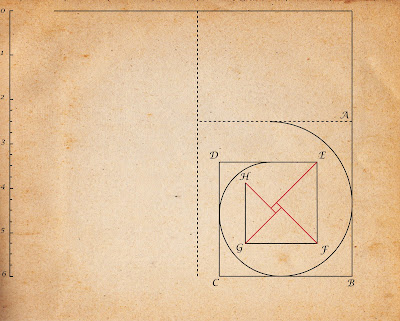
Step 3: Next, draw lines through the points ABCD at 45º [Fig. 3] to where they intersect to form a rectangle in the middle.
 |
| Fig. 4 |
 |
| Fig. 5 |
 |
| Fig. 6 |
According to our 7 : 6 ratio, DE = 2.2cm [CD ÷ 1.16666666].
EF = DE ÷ 1.16666666 = 1.9cm.
FG = EF ÷ 1.16666666 = 1.6cm.
GH = FG ÷ 1.16666666 = 1.37cm
 |
| Fig. 7 |
 |
| Fig. 8 |
 |
| Fig. 9 |
 |
| Fig. 10 |
 |
| Fig. 11 |
Step 11: I could have just stopped at Step 10, but I'm going to add two more steps. I want to extend and soften the curve at the top (or the "thread", to borrow a term from a stair-makers lexicon). This will make it look more like the acanthus scroll. In order to do that, take the line that passed through Point 6 and Point 1 [Fig. 11] and extend it out to the left. Here's where a little creativity comes in. Draw a line at 45º that intersects with your horizontal line at point a'. You can position that line wherever you want.
Now draw an arc centered on Point a', that goes from Point 1 and stops where it intersects the 45º line.
 |
| Fig. 12 |
Here is the completed scroll without all the construction lines, and with one of the beautiful ornament drawings of the acanthus scroll from a previous blog post superimposed for comparison:
































I hate math, but I am squealing with delight over this post!!!!!!!!!! I have played around with only a few steps of this in the past. Thanks Alan for posting this.
ReplyDeleteI loved this whole article!
ReplyDeleteThanks. As Winnie the Pooh once said to Christopher Robin "I am a bear of little brain".
ReplyDeleteMonths later... just to say a big THANKS for posting this. Very interesting/useful !
ReplyDeleteThanks Syrah,
ReplyDeleteI just re-read it also after months, and have absolutely no idea what I was talking about.
Made me laugh!
DeleteMUY BUENA EXPLICACION, DESDE VENEZUELA ESCULTOR HUMBERTO ANTONIO
ReplyDeleteGRACIAS
This is Vitruvius method which produces up to two windings the actual classical spiral has more sometimes as many as 4.
ReplyDeleteThanks, anonymous. I figured that after 2 full turns that people would get the idea. If you want to make more turns, simply repeat the steps.
ReplyDeleteBut heres the trick. In Vitruvius books De architecture he explains same method as you but, the size of the circle in the center of the spiral is 1/18 Diameter of column and the height of the spiral itself is 1/2 Diameter of column So after 3 spirals you have no more room to go. so you cant repeat any more steps. The Classical Eye of Volute had sometimes as many as 4 spirals and it is still unknown how the classical people achieved this some say they would draw it by hand but that is highly unlikely since the carvings were precise.
ReplyDeleteExcellent job
ReplyDeleteI'm so excited you did this series, as I want to use them in home decorating. This one looks like the Greeks disguised their connection to the Egyptians. The use of the ammonite became so obscure that it took me several years from first hearing that people worshiped on them to finding out that they were part of Egypt's belief that to be around the Fibonacci represented in nature would uplift people spiritually. Hindus see the fossils' age as inspiring to remember eternity, as well. Probably the Greeks saw some political advantage in using leaves, rather than fossils.
ReplyDeleteInteresting !
ReplyDeletehttps://bayanlarsitesi.com/
ReplyDeleteGöktürk
Yenidoğan
Şemsipaşa
Çağlayan
4W4U
Malatya
ReplyDeleteKırıkkale
Aksaray
Bitlis
Manisa
L8İKDP
görüntülü show
ReplyDeleteücretlishow
50CU2
https://titandijital.com.tr/
ReplyDeletekars parça eşya taşıma
konya parça eşya taşıma
çankırı parça eşya taşıma
yalova parça eşya taşıma
FZT5Fİ
Mersin Lojistik
ReplyDeleteAmasya Lojistik
Kayseri Lojistik
Kırklareli Lojistik
Erzurum Lojistik
HN17
BDF25
ReplyDeleteBibox Güvenilir mi
Yozgat Lojistik
Amasya Parça Eşya Taşıma
Mercatox Güvenilir mi
Denizli Parça Eşya Taşıma
Karapürçek Parke Ustası
Batman Şehir İçi Nakliyat
Kastamonu Lojistik
Zonguldak Şehirler Arası Nakliyat
4A28A
ReplyDeleteDüzce Lojistik
Çerkezköy Bulaşık Makinesi Tamircisi
Eryaman Boya Ustası
Bitlis Lojistik
Konya Şehirler Arası Nakliyat
Mersin Şehirler Arası Nakliyat
Çerkezköy Kombi Servisi
Muğla Parça Eşya Taşıma
Artvin Parça Eşya Taşıma
7F170
ReplyDeleteAydın Evden Eve Nakliyat
Tekirdağ Parke Ustası
Sakarya Evden Eve Nakliyat
Ünye Marangoz
Çerkezköy Çekici
Huobi Güvenilir mi
Balıkesir Evden Eve Nakliyat
Van Parça Eşya Taşıma
Ankara Şehir İçi Nakliyat
BFF61
ReplyDeleteBitmex Güvenilir mi
Yozgat Şehirler Arası Nakliyat
Trabzon Lojistik
Hatay Parça Eşya Taşıma
Tokat Lojistik
Keçiören Boya Ustası
Isparta Evden Eve Nakliyat
Bitlis Şehirler Arası Nakliyat
Kırşehir Parça Eşya Taşıma
0B60F
ReplyDeleteBitlis Lojistik
Isparta Evden Eve Nakliyat
Manisa Parça Eşya Taşıma
Bilecik Şehirler Arası Nakliyat
Elazığ Evden Eve Nakliyat
Çerkezköy Oto Elektrik
Çerkezköy Çilingir
Adıyaman Lojistik
Rize Parça Eşya Taşıma
7AAE0
ReplyDeletedeca durabolin for sale
Bolu Evden Eve Nakliyat
order peptides
Ünye Evden Eve Nakliyat
Osmaniye Evden Eve Nakliyat
order testosterone enanthate
Çerkezköy Çatı Ustası
Sivas Evden Eve Nakliyat
anapolon oxymetholone for sale
B68F2
ReplyDeletehttps://referanskodunedir.com.tr/
4B1AC
ReplyDeletekilis canlı görüntülü sohbet siteleri
bitlis sohbet sitesi
Karaman Rastgele Görüntülü Sohbet
canlı sohbet siteleri
mobil sohbet sitesi
ığdır telefonda görüntülü sohbet
tekirdağ ücretsiz sohbet uygulaması
yabancı görüntülü sohbet uygulamaları
Istanbul Canlı Sohbet Sitesi
8D762
ReplyDeleteigdir rastgele sohbet uygulaması
aksaray canlı sohbet
canlı sohbet sitesi
kastamonu yabancı görüntülü sohbet
manisa rastgele sohbet
en iyi ücretsiz görüntülü sohbet siteleri
rastgele sohbet uygulaması
sesli sohbet siteleri
Aksaray Kadınlarla Ücretsiz Sohbet
F43DF
ReplyDeleteEskişehir Rastgele Canlı Sohbet
rastgele sohbet uygulaması
en iyi görüntülü sohbet uygulamaları
izmir sohbet odaları
görüntülü sohbet uygulamaları ücretsiz
mobil sohbet siteleri
rastgele sohbet odaları
düzce muhabbet sohbet
Eskişehir Sesli Görüntülü Sohbet
97EB2
ReplyDeletesesli mobil sohbet
ığdır Telefonda Görüntülü Sohbet
rastgele sohbet
yalova rastgele görüntülü sohbet
canlı sohbet siteleri ücretsiz
ucretsiz sohbet
giresun canlı sohbet et
karaman görüntülü sohbet canlı
canlı sohbet odası
B1F2A
ReplyDeleteBitcoin Mining Nasıl Yapılır
Sohbet
Snapchat Takipçi Hilesi
Hamster Coin Hangi Borsada
Lovely Coin Hangi Borsada
Linkedin Takipçi Satın Al
Tumblr Beğeni Hilesi
Twitter Trend Topic Hilesi
Pi Network Coin Hangi Borsada
F6AC8
ReplyDeleteBinance Borsası Güvenilir mi
Bitcoin Madenciliği Siteleri
Bitcoin Kazma
Periscope Takipçi Satın Al
Onlyfans Takipçi Satın Al
Telcoin Coin Hangi Borsada
Tumblr Takipçi Hilesi
Mith Coin Hangi Borsada
Twitter Trend Topic Satın Al
9A740
ReplyDeleteTelegram Görüntüleme Hilesi
Tiktok Beğeni Satın Al
Instagram Beğeni Satın Al
Telegram Görüntüleme Satın Al
Mefa Coin Hangi Borsada
Sohbet
Telegram Abone Hilesi
Bitcoin Nasıl Kazılır
Facebook Takipçi Satın Al
EC694
ReplyDeleteGörüntülü Sohbet
Kripto Para Nasıl Alınır
Bitcoin Nasıl Para Kazanılır
Parasız Görüntülü Sohbet
Facebook Sayfa Beğeni Satın Al
Binance Ne Kadar Komisyon Alıyor
Okex Borsası Güvenilir mi
Sweat Coin Hangi Borsada
Binance Referans Kodu
BD78F382E2
ReplyDeletegüvenilir show
8867E63B97
ReplyDeletetwitter ucuz takipçi
instagram beğeni satın al
türk takipçi
türk takipçi
instagram takipçi
9A57E16311
ReplyDeletetwitter bot takipçi
instagram beğeni satın al
gerçek takipçi
gerçek takipçi
gerçek takipçi
5D3137D965
ReplyDeletemmorpg oyunlar
sms onay
mobil ödeme bozdurma
takipçi satın alma
-